Capitolo 9 Matrici

Le matrici sono una struttura di dati bidimensionale, dove gli elementi sono disposti secondo righe e colonne. Possiamo quindi immaginare una matrice generica di m righe e n colonne in modo simile a quanto rappresentato in Figura 9.1.

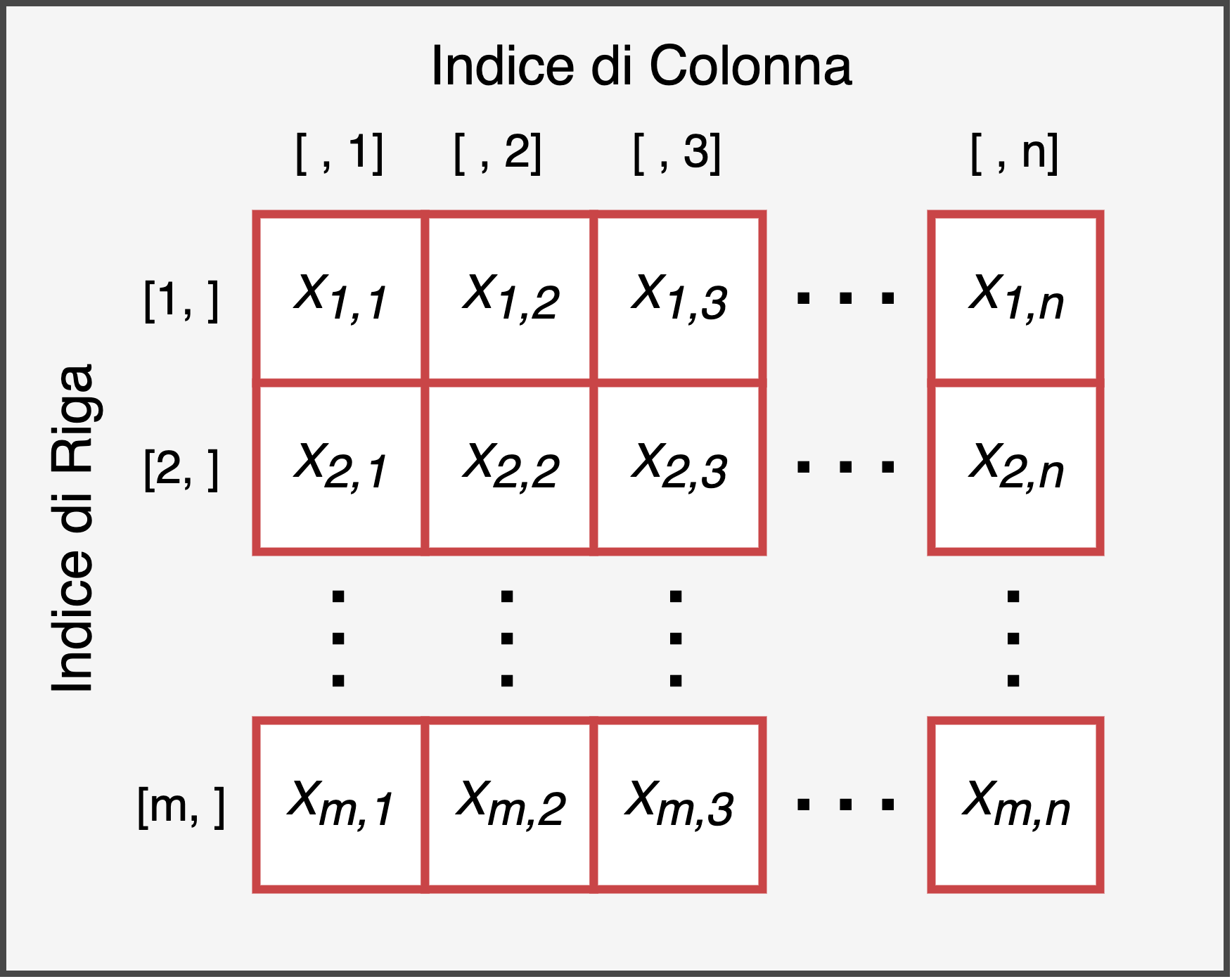
Figure 9.1: Rappresentazione della struttura di una matrice di m colonne e n righe

Due caratteristiche importanti di una matrice sono:

la dimensione - il numero di righe e di colonne da cui è formata la matrice
la tipologia - la tipologia di dati che sono contenuti nella matrice. Infatti, in modo analogo a quanto visto con i vettori, una matrice deve esssere formata da elementi tutti dello stesso tipo. Pertanto esistono diverse tipologie di matrici a seconda del tipo di dati da cui è formata, in particolare abbiamo matrici numeriche, di valori logici e di caratteri (vedi Capitolo 9.1.1).

E’ fondamentale inoltre sottolineare come ogni elemento di una matrice sia caratterizzato da:

un valore - ovvero il valore dell’elemento che può essere di qualsiasi tipo ad esempio un numero o una serie di caratteri.
un indice di posizione - ovvero una coppia di valori (i, j) interi positivi che indicando rispettivamente l’indice di riga e l’indice di colonna e che permettono di identificare univocamente l’elemento all’interno della matrice.

Ad esempio, data una matrice \(X\) di dimensione \(3\times4\) (i.e., 3 righe e 4 colonne) così definita: \[ X = \begin{bmatrix} 3 & 12 & 7 & 20\\ 16 & 5 & 9 & 13\\ 10 & 1 & 14 & 19 \end{bmatrix}, \] abbiamo che \(x_{2, 3} = 9\) mentre \(x_{3, 2} = 1\). Questo ci serve solo per ribadire il corretto uso degli indici, dove per un generico elemento \(x_{i, j}\), il valore i è l’indice di riga mentre il valore j è l’indice di colonna. Prima si indicano le righe poi le colonne.

Vediamo ora come creare delle matrici in R e come compiere le comuni operazini di selezione. Successivamente vedremo diverse manipolazioni e operazioni con le matrici. Infine estenderemo brevemente il concetto di matrici a dimensioni maggiori di due atttraverso l’uso degli array.

9.1 Creazione

Il comando usato per creare una matrice in R è matrix() e contiene diversi argomenti:

nome_matrice <- matrix(data, nrow = , ncol = , byrow = FALSE)

data - un vettore di valori utilizzati per popolare la matrice
nrow e ncol - sono rispettivamente il numero di righe e il numero di colonne della matrice
byrow - indica se la matrice deve essere popolata per riga oppure per colonna. Il valore di default è FALSE quindi i valori della matrice vengono aggiunti colonna dopo colonna. Indicare TRUE per aggiungere gli elementi riga dopo riga

Creiamo come esempio una matrice di 3 righe e 4 colonne con i valori che vanno da 1 a 12.

# Dati per popolare la matrice
my_values <- 1:12
my_values
##  [1]  1  2  3  4  5  6  7  8  9 10 11 12

# Matrice popolata per colonne
mat_bycol <- matrix(my_values, nrow = 3, ncol = 4)
mat_bycol
##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12

La funzione matrix() ha di default l’argomento byrow = FALSE, quindi di base R popola le matrici colonna dopo colonna. Per popolare le matrici riga dopo riga invece, è necessario richiederlo esplicitamente specificando byrow = TRUE.

# Matrice popolata per righe
mat_byrow <- matrix(my_values, nrow = 3, ncol = 4, byrow = TRUE)
mat_byrow
##      [,1] [,2] [,3] [,4]
## [1,]    1    2    3    4
## [2,]    5    6    7    8
## [3,]    9   10   11   12

E’ importante notare come mentre sia possibile specificare qualsiasi combinazione di righe e colonne, il numero di valori forniti per popolare la matrice deve essere compatibile con la dimensione della matrice. In altre parole, non posso fornire più o meno dati di quelli che la matrice può contenere.

Pertanto, la launghezza del vettore passato all’argomento data deve essere compatibile con gli argomenti nrow e ncol. E’ possibile tuttavia, fornire un unico valore se si desidera ottenre una matrice in cui tutti i valori siano identici. Creiamo ad esempio una matrice vuota con soli valori NA con 3 righe e 3 colonne.

mat_NA <- matrix(NA, nrow = 3, ncol = 3)
mat_NA
##      [,1] [,2] [,3]
## [1,]   NA   NA   NA
## [2,]   NA   NA   NA
## [3,]   NA   NA   NA

In realtà è possibile fornire più o meno dati di quelli che la matrice può contenere. Nel caso vengano forniti più valori, R semplicemente utilizza i primi valori disponibili ignorando quelli successivi.

matrix(1:20, nrow = 2, ncol = 2)
##      [,1] [,2]
## [1,]    1    3
## [2,]    2    4

Nel caso vengano forniti meno valori, invece, R riutilizza gli stessi valori nello stesso ordinere per completare la matrice avvertendoci del problema.

matrix(1:4, nrow = 3, ncol = 4)
##      [,1] [,2] [,3] [,4]
## [1,]    1    4    3    2
## [2,]    2    1    4    3
## [3,]    3    2    1    4

Tuttavia, è meglio evitare questa pratica di ciclare i valori poichè i risultati potrebbero essere poco chiari ed è facile commettere errori.

9.1.1 Tipologie di Matrici

Abbiamo viso che, in modo analogo ai vettori, anche per le matrici è necessario che tutti i dati siano della stessa tipologia. Avremo pertanto matrici che includono solo valori character, double, integer oppure logical e le operazioni che si potranno eseguire (uso di operatori matematiche o operatori logici-relazionali) dipenderanno dalla tipologia di dati. Tuttavia, a differenza dei vettori, la tipologia di oggetto rimarrà sempre matrix indipendentemente dai dati contenuti. Le matrici sono sempre matrici, è la tipologia di dati che varia.

Character

E’ possibile definire una matrice di soli caratteri, tuttavia sono usate raramente visto che chiaramente tutte le operazioni matematiche non sono possibili.

mat_char <- matrix(letters[1:12], nrow = 3, ncol = 4, byrow = TRUE)
mat_char
##      [,1] [,2] [,3] [,4]
## [1,] "a"  "b"  "c"  "d" 
## [2,] "e"  "f"  "g"  "h" 
## [3,] "i"  "j"  "k"  "l"

class(mat_char)
## [1] "matrix" "array"
typeof(mat_char)
## [1] "character"

In R esistono due speciali oggetti letters e LETTERS che includono rispettivamente le lettere minuscole e maiuscole dell’alfabeto inglese.

letters[1:5]
## [1] "a" "b" "c" "d" "e"
LETTERS[6:10]
## [1] "F" "G" "H" "I" "J"

Numeric

Le matrici di valori numerici, sia double che integer, sono senza dubbio le più comuni ed utilizzate. Vengono spesso sfruttate per eseguire calcoli algebrici computazionalemnte molto efficienti.

# doubles
mat_num <- matrix(5, nrow = 3, ncol = 4)
class(mat_num)
## [1] "matrix" "array"
typeof(mat_num)
## [1] "double"

# integers
mat_int <- matrix(5L, nrow = 3, ncol = 4)
class(mat_int)
## [1] "matrix" "array"
typeof(mat_int)
## [1] "integer"

Logical

Infine le matrici possono essere formate anche da valori logici TRUE e FALSE. Vedremo un loro importante utilizzo per quanto riguarda la selezione degli elementi di una matrice nel Capitolo 9.2.1.

mat_logic <- matrix(c(TRUE, FALSE), nrow = 3, ncol = 4)
mat_logic
##       [,1]  [,2]  [,3]  [,4]
## [1,]  TRUE FALSE  TRUE FALSE
## [2,] FALSE  TRUE FALSE  TRUE
## [3,]  TRUE FALSE  TRUE FALSE
class(mat_logic)
## [1] "matrix" "array"
typeof(mat_logic)
## [1] "logical"

Ricordiamo che è comunque possibile eseguire operazioni matematiche con i valori logici poichè verranno automaticamente rasformatti nei rispettivi valori numerici 1 e 0.

Esercizi

Esegui i seguenti esercizi (soluzioni): 1. Crea la matrice A così definita:

\[ \begin{matrix} 2 & 34 & 12 & 7\\ 46 & 93 & 27 & 99\\ 23 & 38 & 7 & 04 \end{matrix} \]

Crea la matrice B contenente tutti i primi 12 numeri dispari disposti su 4 righe e 3 colonne.
Crea la matrice C contenente i primi 12 multipli di 9 disposti su 3 righe e 4 colonne.
Crea la matrice D formata da 3 colonne in cui le lettere "A","B" e "C" vengano ripetute 4 volte ciascuna rispettivamente nella prima, seconda e terza colonna.
Crea la matrice E formata da 3 righe in cui le lettere "A","B" e "C" vengano ripetute 4 volte ciascuna rispettivamente nella prima, seconda e terza riga.

9.2 Selezione Elementi

L’aspetto sicuramente più importante (e divertente) riguardo le matrici è accedere ai vari elementi. Ricordiamo che una matrice non è altro che una griglia di righe e colonne dove vengono disposti i vari valori. Indipendentemente da cosa la matrice contenga, è possibile utilizzare gli indici di riga e di colonna per identificare univocamente un dato elemento nella matrice. Pertanto ad ogni elemento è associata una coppia di valori (i, j) dove i è l’indice di riga e j è l’indice di colonna.

Per visualizzare questo concetto, riportiamo nel seguente esempio gli indici per ogni elemnto di una matrice \(3\times4\):

##      [,1]  [,2]  [,3]  [,4] 
## [1,] "1,1" "1,2" "1,3" "1,4"
## [2,] "2,1" "2,2" "2,3" "2,4"
## [3,] "3,1" "3,2" "3,3" "3,4"

In R è possibile selezionare un elemento di una matrice utilizzando il suo indice di riga e di colonna. In modo analogo ai vettori è necessario quindi indicare all’inerno delle parentesi quadre [] poste dopo il nome del vettore, l’indice di riga e l’indice di colonna separati da virgola.

nome_matrice[<indice-riga>, <indice-colonna>]

L’ordine [<indice-riga>, <indice-colonna>] è prestabilito e deve essere rispettato affinché la selezione avvenga correttamente. Vediamo un semplice esempio di come sia possibile accedere ad un qualsiasi elemento:

my_matrix <- matrix(1:12, nrow = 3, ncol = 4)
my_matrix
##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12

# Selezioniamo l'elemento alla riga 2 e colonna 3
my_matrix[2,3]
## [1] 8

# Selezioniamo il valore 6
my_matrix[3,2]
## [1] 6

Notiamo come indicando degli indici al di fuori della dimensione della matrice otteniamo un messaggio di errore.

my_matrix[20,30]
## Error in my_matrix[20, 30]: subscript out of bounds

Oltre alla selezione di un singolo elemento è possibile eseguire altri tipi di selezione:

Selezionare Riga o Colonna

E’ possibile selezionare tutti gli elementi di una riga o di una colonna utilizzando la seguente sintassi:

# Selzione intera riga
nome_matrice[<indice-riga>, ]

# Selzione intera colonna
nome_matrice[ , <indice-colonna>]

Nota come sia comunque necessario l’utilizzo della virgola lasciando vuoto il posto prima o dopo la virgola per indicare ad R di selezionare rispettivamente tutte le righe o tutte le colonne.

# Selezioniamo la 2 riga e tutte le colonne
my_matrix[2, ]
## [1]  2  5  8 11

# Selezioniamo  tutte le righe e la 3 colonna
my_matrix[ ,3]
## [1] 7 8 9

Qualora fosse necessario selezionare più righe o più colonne è sufficiente indicare tutti gli indici di interesse. Ricorda che questi devono essere specificati in un unico vettore. All’interno delle parentesi quadre, R si aspetta una sola virgola che separa gli indici di riga da quelli di colonna. E’ quindi necessario combinare gli indici che vogliamo selezionare in un unico vettore sia nel caso delle righe che delle colonne. Per selezionare righe o colonne in successione, ad esempio le prime 3 colonne, posso utilizzare la scrittura compatta 1:3 che è equivalente a c(1,2,3).

# Selezioniamo la 1 e 3 riga
my_matrix[c(1,3), ]
##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    3    6    9   12

# Selezioniamo dalla 2° alla 4° colonna
my_matrix[ , 2:4]
##      [,1] [,2] [,3]
## [1,]    4    7   10
## [2,]    5    8   11
## [3,]    6    9   12

Selezionare Regione Matrice

Combinando indici di righe e di colonne è anche possibile selezionare specifiche regioni di una matrice o selezionare alcuni suoi valori per creare una nuova matrice.

# Selezioniamo un blocco
my_matrix[1:2, 3:4]
##      [,1] [,2]
## [1,]    7   10
## [2,]    8   11

# Selezioniamo valori sparsi
my_matrix[c(1,3), c(2,4)]
##      [,1] [,2]
## [1,]    4   10
## [2,]    6   12

Ricordiamo che, come per i vettori, l’operazione di selezione non modifichi l’oggetto iniziale. Pertanto è necessario salvare il risultato della selezione se si desidera mantenere le modifiche.

I più attenti avranno notato che che i comandi di selezione non restituiscono sempre lo stesso oggetto, a volte otteniamo come risultato un vettore e delle altre una matrice.

E’ importante chiarire che una un vettore non è un matrice e tanto più vale l’opposto. In R questi sono due tipologie di oggetti diversi e sarà importante tenere a mente questa distinzione.

# Un vettore non è una matrice
my_vector <- 1:5
is.vector(my_vector) # TRUE
is.matrix(my_vector) # FALSE

# Una matrice non è un vettore
my_matrix <- matrix(1, nrow = 3, ncol = 3)
is.vector(my_matrix) # FALSE
is.matrix(my_matrix) # TRUE

Il risultato che otteniamo da una selezione potrebbe essere un vettore oppure una matrice a seconda del tipo di selezione. Vediamo in particolare come selezionando un’unica colonna (o riga) otteniamo un vettore mentre selezionando più colonne (o righe) otteniamo una matrice.

# Seleziono una colonna
is.vector(my_matrix[, 1]) # TRUE
is.matrix(my_matrix[, 1]) # FALSE

# Seleziono più colonne
is.vector(my_matrix[, c(1,2)]) # FALSE
is.matrix(my_matrix[, c(1,2)]) # TRUE

Questa distinzione influirà sul successivo utilizzo dell’oggetto ottenuto dalla selezione.

Vettore Riga e Vettore Colonna

Una particolare fonte di incomprensioni e successivi errori riguarda proprio l’utilizzo di un vettore ottenuto dalla selezione di una singola riga (o una singola colonna) di una matrice come fosse un vettore riga (o un vettore colonna).

In algebra lineare, i vettori riga ed i vettori colonna non sono altro che delle matrici rispettivamente di dimensione \(1\times n\) e \(m \times 1\). La dimensione (\(righe \times colonne\)) di una matrice, e quindi anche di un vettore, rivestono un ruolo importante nelle operazioni con le matrici ed in particolare nel prodotto matriciale.

In R i vettori hanno una sola dimensione ovvero la lunghezza e quindi nel loro utilizzo con operazioni tra matrici vengono convertiti automaticamente in vettori riga o vettori colonna a seconda delle necessità. Tuttavia, questa trasformazione potrebbe non sempre rispettare le attuali intenzioni ed è quindi meglio utlizzare sempre le matrici e non i vettori.

# Vettore
my_vector <- 1:4
dim(my_vector) # dimensione righe, colonne
## NULL
length(my_vector)
## [1] 4

# Matrice 1x4 (vettore riga)
my_row_vector <- matrix(1:4, nrow = 1, ncol = 4)
dim(my_row_vector) 
## [1] 1 4
my_row_vector
##      [,1] [,2] [,3] [,4]
## [1,]    1    2    3    4

# Matrice 4x1 (vettore colonna)
my_col_vector <- matrix(1:4, nrow = 4, ncol = 1)
dim(my_col_vector) 
## [1] 4 1
my_col_vector
##      [,1]
## [1,]    1
## [2,]    2
## [3,]    3
## [4,]    4

Srotolare una Matrice

Abbiamo visto che possiamo facilmente popolare una matrice con un vettore. Allo stesso modo possiamo vettorizzare una matrice (in altri termini “srotolare” la matrice) per ritornare al vettore originale. Con il comando c(matrice) oppure forzando la tipologia di oggetto a vettore con vector(matrice) o as.vector(matrice).

# Da matrice a vettore
my_matrix <- matrix(1:12, nrow = 3, ncol = 4)
c(my_matrix)
##  [1]  1  2  3  4  5  6  7  8  9 10 11 12
as.vector(my_matrix)
##  [1]  1  2  3  4  5  6  7  8  9 10 11 12

9.2.1 Utilizzi Avanzati Selezione

Vediamo ora alcuni utilizzi avanzati della selezione di elementi di una matrice. In particolare impareremo a:

utilizzare gli operatori relazionali e logici per selezionare gli elementi di una martrice
modificare l’ordine di righe e colonne
sostituire degli elementi
eliminare delle righe o colonne

Nota che queste operazioni siano analoghe a quelle viste per i vettori e quindi seguiranno le stesse regole e principi.

Operatori Relazionali e Logici

Un’utile funzione è quella di selezionare tra gli elementi di una matrice quelli che rispetano una certa condizione. Possiamo ad esempio valutare “quali elementi della matrice sono maggiori di x?”. Per fare questo dobbiamo specificare all’interno delle parentesi quadre la proposizione di interesse utilizzando gli operatori relazionali e logici (vedi Capitolo 3.2).

Quando una matrice è valutata all’interno di una proposizione, R valuta la veridicità di tale proposizione rispetto ad ogni suo elemento. Come risultato otteniamo una matrice di valori logici con le rispettive risposte per ogni elemento (TRUE o FALSE).

my_matrix <- matrix(1:23, nrow = 3, ncol = 4)
## Warning in matrix(1:23, nrow = 3, ncol = 4): data length [23] is not a sub-
## multiple or multiple of the number of rows [3]
my_matrix
##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12

# Elemeni maggiori di 4 e minori di 10
test <- my_matrix >= 4 & my_matrix <=10
test
##       [,1] [,2] [,3]  [,4]
## [1,] FALSE TRUE TRUE  TRUE
## [2,] FALSE TRUE TRUE FALSE
## [3,] FALSE TRUE TRUE FALSE

Questa matrice può essere utilizzata all’interno delle parentesi quadre per selezionare gli elementi della matrice originale che soddisfano la proposizione. Gli elementi associati al valore TRUE sono selezionati mentre quelli associati al valore FALSE sono scartati.

# Seleziono gli elementi
my_matrix[test]
## [1]  4  5  6  7  8  9 10

Nota come in questo caso non sia necessaria alcuna virgola all’interno delle parentesi quadre e come il risultato ottenuto sia un vettore.

Modificare Ordine Righe e Colonne

Gli indici di riga e di colonna possono essere utilizzati per riordinare le righe e le colonne di una matrice a seconda delle necessità.

my_matrix <- matrix(1:6, nrow = 3, ncol = 4)
my_matrix
##      [,1] [,2] [,3] [,4]
## [1,]    1    4    1    4
## [2,]    2    5    2    5
## [3,]    3    6    3    6

# Altero l'ordinen delle righe
my_matrix[c(3,2,1), ]
##      [,1] [,2] [,3] [,4]
## [1,]    3    6    3    6
## [2,]    2    5    2    5
## [3,]    1    4    1    4

# Altero l'ordine delle colonnne
my_matrix[ ,c(1,3,2, 4)]
##      [,1] [,2] [,3] [,4]
## [1,]    1    1    4    4
## [2,]    2    2    5    5
## [3,]    3    3    6    6

Modificare gli Elementi

Un importante utilizzo degli indici riguarda la modifica di un elemento di una matrice. Per sostituire un vecchio valore con un nuovo valore, seleziono il vecchio valore della matrice e utilizzo la funzione <- (o =) per assegnare il nuovo valore.

my_matrix <- matrix(1:12, nrow = 3, ncol = 4)
my_matrix
##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12

# Modifico il l'elemento con il valore 5
my_matrix[2,2] <- 555
my_matrix
##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2  555    8   11
## [3,]    3    6    9   12

E’ possibile anche sostituire tutti i valori di un’intera riga o colonnna opportunamente selezionata. In questo caso sarà necessario fornire un corretto numero di nuovi valori da utilizzare.

# Modifico la 2 colonna
my_matrix[ ,2] <- c(444, 555, 666)
my_matrix
##      [,1] [,2] [,3] [,4]
## [1,]    1  444    7   10
## [2,]    2  555    8   11
## [3,]    3  666    9   12

# Modifico la 3 riga
my_matrix[3, ] <- c(111, 666, 999, 122)
my_matrix
##      [,1] [,2] [,3] [,4]
## [1,]    1  444    7   10
## [2,]    2  555    8   11
## [3,]  111  666  999  122

Nota come a differenza dei vettori non sia possibile aggiungere una nuova riga o colonna attraverso questa operazione ma sarà necesssario utilizzare una diversa procedura (vedi Capitolo 9.3.2).

# Aggiungo una nuova colona [errore selezione indici]
my_matrix[, 5] <- c(27, 27, 27)
## Error in `[<-`(`*tmp*`, , 5, value = c(27, 27, 27)): subscript out of bounds

Eliminare Righe o Colonne

Per eliminare delle righe (o delle colonne) da una matrice, è necessario indicare all’interno delle parentesi quadre gli indici di riga (o di colonna) che si intende eliminare, preceduti dall’operatore - (meno). Nel caso di più righe (o colone) è possibile indicare il meno solo prima del comando c() analogamente con quanto fatto con i vettori.

my_matrix <- matrix(1:12, nrow = 3, ncol = 4)

# Elimino la 2° riga
my_matrix[-2, ]
##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    3    6    9   12

# Elimino la 2° riga  e la 2° e 3° colonna
my_matrix[-2, -c(2,3)]
##      [,1] [,2]
## [1,]    1   10
## [2,]    3   12

Nota come l’operazione di eliminazione sia comunque un’operazione di selezione. Pertanto è necessario salvare il risultato ottenuto se si desidera mantenere le modifiche.

Esercizi

Utilizzando le matrici create nei precedenti esercizi esegui le seguenti consegne (soluzioni):

Utilizzando gli indici di riga e di colonna selziona il numero 27 della matrice A
Selziona gli elementi compresi tra la seconda e quarta riga, seconda e terza colonna della matrice B
Seleziona solo gli elementi pari della matrice A (Nota: utilizza l’operazione resto %%)
Elimina dalla matrice C la terza riga e la terza colonna
Seleziona tutti gli elementi della seconda e terza riga della matrice B
Seleziona tutti gli elementi diversi da “B” appartenenti alla matrice D

9.3 Funzioni ed Operazioni

Vediamo ora alcune funzioni frequentemente usate e le comuni operazioni eseguite con le matrici (vedi Tabella 9.1).

Table 9.1: Funzioni e operazioni con matrici
Funzione	Descrizione
nuova_matrice <- cbind(matrice1, matrice2)	Unire due matrici creando nuove colonne (le matrici devono avere lo stesso numero di righe)
nuova_matrice <- rbind(matrice1, matrice2)	Unire due matrici creando nuove righe (le matrici devono avere lo stesso numero di colonne)
nrow(nome_matrice)	Numero di righe della matrice
ncol(nome_matrice)	Numero di colonne della matrice
dim(nome_matrice)	Dimensione della matrice (righe e colonne)
colnames(nome_matrice)	Nomi delle colonne della matrice
rownames(nome_matrice)	Nomi delle righe della matrice
dimnames(nome_matrice)	Nomi delle righe e delle colonne
t(nome_matrice)	Trasposta della matrice
diag(nome_matrice)	Vettore con gli elementi della diagonale della matrice
det(nome_matrice)	Determinante della matrice (la matrice deve essere quadrata)
solve(nome_matrice)	Inversa della matrice
matrice1 + matrice2	Somma elemento per elemento di due matrici
matrice1 - matrice2	Differenza elemento per elemento tra due matrici
matrice1 * matrice2	Prodotto elemento per elemento tra due matrici
matrice1 / matrice2	Rapporto elemento per elemento tra due matrici
matrice1 %*% matrice2	Prodotto matriciale

Descriviamo ora nel dettaglio alcuni particolari utilizzi.

9.3.1 Attributi di una Matrice

Abbiamo visto nel Capitolo 8.1 che gli oggetti in R possiedono quelli che sono definiti attributi ovvero delle utili informazioni riguardanti l’oggetto stesso, una sorta di metadata. Vediamo ora alcuni attributi particolarmente rilevanti nel caso delle matrici ovvero la dimensione (dim) e i nomi delle righe e colonne (names).

Dimensione

Ricordiamo che la matrice è un oggetto bidimensionale formato da righe e colonne. Queste formano pertanto le dimensioni di una matrice. Per ottenere il numero di righe e di colonne di una matrice, possiamo usare rispettivamente i comandi nrow() e ncol().

my_matrix <- matrix(1:12, ncol = 3, nrow = 4)

# Numero di righe
nrow(my_matrix)
## [1] 4

# Numero di colonne
ncol(my_matrix)
## [1] 3

In alternativa per conoscere le dimensioni di una matrice è possibile utilizzare la funzione dim(). Questa ci restituirà un vettore con due valori dove il primo rappresenta il numero di righe e il secondo il numero di colonne.

dim(my_matrix)
## [1] 4 3

Nomi Righe e Colonne

Come avrete notato, di base le dimensioni di una matrice (ovvero le righe e le colonne) vengono identificate attraverso i loro indici numerici. In R tuttavia, è anche possibile assegnare dei nomi alle righe e alle colonne di una matrice.

Con i comandi rownames() e colnames() possiamo accedere rispettivamente ai nomi delle righe e delle colonne.

my_matrix <- matrix(1:12, nrow = 3, ncol = 4)

# Nome di righe
rownames(mat)
## NULL

# Nome di colonne
colnames(mat)
## NULL

Non essendo impostati, ottieniamo inizialmente come output il valore NULL. Per impostare i nomi di righe e/o colonne, sarà quindi necessario assegnare a rownames(nome_matrice) e colnames(nome_matrice) un vettore di caratteri della stessa lunghezza della dimensione che stiamo rinominando. Se impostiamo un unico carattere, tutte le righe/colonne avranno lo stesso valore. Questo ci fa capire che, se vogliamo impostare dei nomi, R richiede che questo venga fatto per tutte le righe/colonne.

# Assegnamo i nomi alle righe
rownames(my_matrix) <- LETTERS[1:3]
my_matrix
##   [,1] [,2] [,3] [,4]
## A    1    4    7   10
## B    2    5    8   11
## C    3    6    9   12

# Assegno i nomi alle colonne
colnames(my_matrix) <- LETTERS[4:7]
my_matrix
##   D E F  G
## A 1 4 7 10
## B 2 5 8 11
## C 3 6 9 12

In alternativa posso utilizzare il dimnames() per accedere contemporaneamente sia ai nomi di riga che a quelli di colonna. Come output ottengo una lista (vedi Capitolo 11) dove vengono prima indicati i nomi di riga e poi quelli di colonna

dimnames(my_matrix)
## [[1]]
## [1] "A" "B" "C"
## 
## [[2]]
## [1] "D" "E" "F" "G"

Quando nel Capitolo 9.2 abbiamo visto i diversi modi di selezionare gli elementi di una matrice, abbiamo sempre usato gli indici numerici di riga e di colonna. Tuttavia, quando i nomi delle delle dimensioni sono disponibili, è possibile indicizzare una matrice in base ai nomi delle righe e/o colone.

Possiamo quindi selezionare la prima colonna sia con il suo indice numerico nome_matrice[ , 1] ma anche con il nome assegnato nome_matrice[ ,"nome_colonna"]. Queste sono operazioni poco utili con le matrici ma che saranno fondamentali nel caso dei dataframe (vedi Capitolo 10).

# Seleziono la colona "F"
my_matrix[ , "F"]
## A B C 
## 7 8 9

# Selezioniamo la riga "A" e "C"
my_matrix[c("A", "C"), ]
##   D E F  G
## A 1 4 7 10
## C 3 6 9 12

9.3.2 Unire Matrici

Abbiamo visto nel Capitolo 7.3 come si possono unire diversi vettori tramite la funnzione c(). Anche per le matrici è possibile combinare matrici diverse, rispettando però alcune regole:

rbind() - Posso unire matrici per riga ovvero aggiungo una o più righe ad una matrice, in questo caso le matrici devono avere lo stesso numero di colonne
cbind() - Posso unire matrici per colonna ovvero aggiungo una o più colonne ad una matrice, in questo caso le matrici devono avere lo stesso numero di righe
Le matrici che unisco devono essere della stessa tipologia (numeri o caratteri)

Quindi, data una matrice my_matrix di dimensione \(m \times n\) se volgiamo aggiungere le righe di una seconda matrice row_matrix possiamo utlizzare il comando rbind(my_matrix, row_matrix) a patto che abbiano lo stesso numero di colonnne (\(n\)). Se vogliamo invece aggiungere le colonne di una nuova matrice col_matrix possiamo utlizzare il comando cbind(my_matrix, col_matrix) a patto che abbiano lo stesso numero di righe (\(m\)). E’ utile pensare all’unione come ad un collage tra matrici. In Figura9.2 è presente uno schema utile per capire visivamente questo concetto, dove le matrici colorate in verde possono essere correttamente unite mentre le matrici in rosso non presentano la corretta dimensionalità.

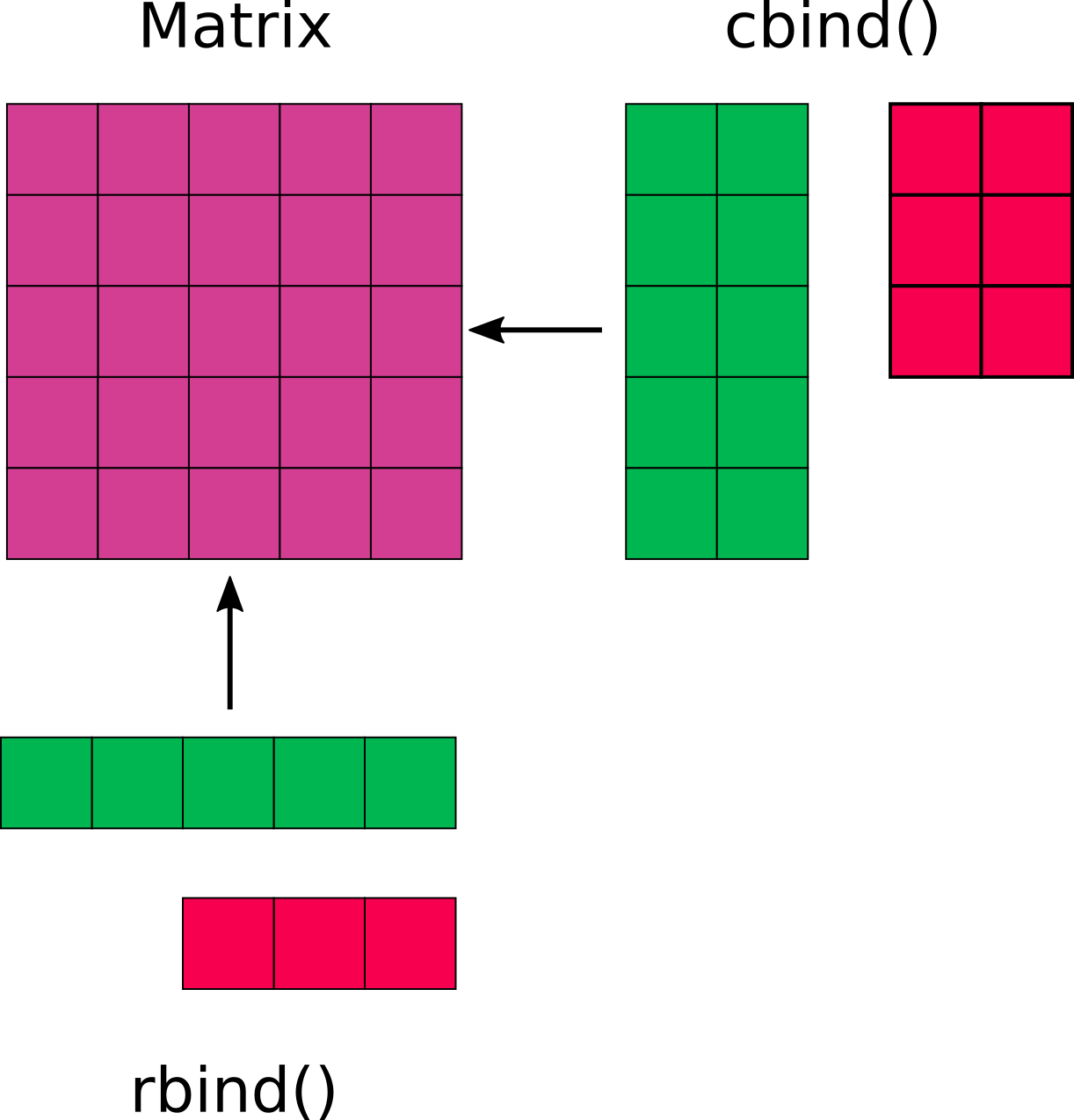
Figure 9.2: Schema per la combinazione di matrici

Vediamo un esempio in R:

# Matrice di partenza
my_matrix <- matrix(1:12, nrow = 3, ncol = 4)
my_matrix
##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12

# Matrice con stesso numero di colonne
row_matrix <- matrix(77, nrow = 2, ncol = 4)
row_matrix
##      [,1] [,2] [,3] [,4]
## [1,]   77   77   77   77
## [2,]   77   77   77   77

# Unione per riga
rbind(my_matrix, row_matrix)
##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12
## [4,]   77   77   77   77
## [5,]   77   77   77   77


# Matrice con stesso numero di righe
col_matrix <- matrix(99, nrow = 3, ncol = 2)
col_matrix
##      [,1] [,2]
## [1,]   99   99
## [2,]   99   99
## [3,]   99   99

# Unione per colonna
cbind(my_matrix, col_matrix)
##      [,1] [,2] [,3] [,4] [,5] [,6]
## [1,]    1    4    7   10   99   99
## [2,]    2    5    8   11   99   99
## [3,]    3    6    9   12   99   99

Un ultimo aspetto utile è l’estensione dei comandi cbind() ed rbind(). Fino ad ora li abbiamo utilizzati con due soli elementi: matrice di partenza e matrice da aggiungere. Tuttavia, è possibile indicare più matrici che si vogliono unire, separandole con una virgola. Se vogliamo combinare \(n\) matrici possiamo usare il comando cbind(mat1, mat2, mat3, ...) o rbind(mat1, mat2, mat3, ...). In questo caso il risultato finale sarà l’unione delle matrici nell’ordine utilizzato nel definire gli argomenti quindi prima la mat1, poi la mat2 e così via.

Abbiamo visto che possiamo unire matrici per riga/colonna solo se il numero di colonne/righe delle due matrici sono equivalenti. Otteniamo un errore, invece, quando cerchiamo di combinare matrici di dimensioni diverse “number of columns/rows of matrices must match”.

my_matrix <- matrix(1:12, nrow = 3, ncol = 4)

# Matrice con errato numero di colonne
wrong_matrix <- matrix(77, nrow = 2, ncol = 7)
rbind(my_matrix, wrong_matrix)
## Error in rbind(my_matrix, wrong_matrix): number of columns of matrices must match (see arg 2)

9.3.3 Operatori Matematici

Gli operatori matematici (e.g., +, -, *, /, etc.) svolgono le operazioni tra una matrice ed un singolo valore, tra una matrice ed un vettore oppure tra due matrici.

Operazione tra Matrice e Valore Singolo

Nel caso di un singolo valore, la stessa operazione viene semplicemente eseguita su tutti gli elementi della matrice. Possiamo ad esempio aggiungere a tutti gli elementi di una matrice il volore 100.

my_matrix <- matrix(1:12, nrow = 3, ncol = 4)
my_matrix
##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12

# Aggiungo 100
my_matrix + 100
##      [,1] [,2] [,3] [,4]
## [1,]  101  104  107  110
## [2,]  102  105  108  111
## [3,]  103  106  109  112

Operazione tra Matrice e Vettore

Nel caso di un vettore, l’operazione viene eseguita elemento per elemento ciclando i valori del vettore qualora la sua lunghezza non sia suficiente. Possiamo ad esempio aggiungere a tutti gli elementi di una matrice il vettore di valori c(100, 200, 300, 400).

# Aggiungo un vettore di valori
my_matrix + c(100, 200, 300, 400)
##      [,1] [,2] [,3] [,4]
## [1,]  101  404  307  210
## [2,]  202  105  408  311
## [3,]  303  206  109  412

Com’è facilmente intuibile, questa operazione è poco connsigliata poichè è facile causa di errori ed incomprensioni.

Operazione tra Matrici

Nel caso di operazioni tra matrici, l’operazione viene eseguita elemento per elemento ed è quindi importante che le matrici abbiano la stessa dimensione. Possiamo ad esempio aggiungere a tutti gli elementi di una matrice nelle cui righe abbiamo i valori 100, 200, 300 e 400.

sum_matrix <- matrix(rep(c(100, 200, 300, 400), each = 3), nrow = 3, ncol = 4)
sum_matrix
##      [,1] [,2] [,3] [,4]
## [1,]  100  200  300  400
## [2,]  100  200  300  400
## [3,]  100  200  300  400

# sommo due matrici
my_matrix + sum_matrix
##      [,1] [,2] [,3] [,4]
## [1,]  101  204  307  410
## [2,]  102  205  308  411
## [3,]  103  206  309  412

Nota come in R l’operatore * indichi il semmplice prodotto elemento per elemento mentre per ottenere il prodotto matriciale è necessario utilizzare l’operatore %*%.

Il prodotto matriciale segue delle specifiche regole e specifiche proprietà. In particolare, il numero di colonne della prima matrice deve essere uguale al numero di righe della seconda matrice. Per un approfondimento vedi https://it.wikipedia.org/wiki/Moltiplicazione_di_matrici.

Algebra Lineare

Anche altri aspetti che riguardano le operazioni con le matrici non vengono qui discusse ma si rimanda il lettore interessato alle seguenti pagine:

Per il significato di determinante di una matrice considera https://it.wikipedia.org/wiki/Determinante
Per il significato di matrice inversa considera https://it.wikipedia.org/wiki/Matrice_invertibile

Diagonale

Vediamo ora alcuni utili funzioni che riguardano la diagonale di una matrice. La diagonale di una matrice è formata dagli elementi i cui indici di riga e di colonna sono uguali, ovvero l’insieme di elementi associati allo stesso indice di riga e colonna (\(x_{i,i}\)).

Il comando diag(nome_matrice) permette di estrarre la diagonale di una matrice e trattarla come un semplice vettore:

# Matrice quadrata
square_matrix <- matrix(1:16, nrow = 4, ncol = 4)
square_matrix
##      [,1] [,2] [,3] [,4]
## [1,]    1    5    9   13
## [2,]    2    6   10   14
## [3,]    3    7   11   15
## [4,]    4    8   12   16

diag(square_matrix)
## [1]  1  6 11 16

# Matrice non quadrata
my_matrix <- matrix(1:12, nrow = 3, ncol = 4)
my_matrix
##      [,1] [,2] [,3] [,4]
## [1,]    1    4    7   10
## [2,]    2    5    8   11
## [3,]    3    6    9   12

diag(my_matrix)
## [1] 1 5 9

La funzione diag() può anche essere usata per sostituire in modo semplice gli elementi sulla diagonale di una matrice oppure per creare una matrice diagonale in cui gli altri valori siano tutti zero, ad esempio la matrice identità.

# Sostituisco gli elementi della diagonale
diag(my_matrix) <- 999
my_matrix
##      [,1] [,2] [,3] [,4]
## [1,]  999    4    7   10
## [2,]    2  999    8   11
## [3,]    3    6  999   12

# Creo una matrice diagonale
diag(4, nrow = 3, ncol = 4)
##      [,1] [,2] [,3] [,4]
## [1,]    4    0    0    0
## [2,]    0    4    0    0
## [3,]    0    0    4    0

# Creo una matrice identità 4X4
diag(4)
##      [,1] [,2] [,3] [,4]
## [1,]    1    0    0    0
## [2,]    0    1    0    0
## [3,]    0    0    1    0
## [4,]    0    0    0    1

Esercizi

Utilizzando le matrici create nei precedenti esercizi, esegui le seguentti consegne (soluzioni):

Crea la matrice G unendo alla matrice A le prime due colonne della matrice C
Crea la matrice H unendo alla matrice C le prime due righe della matrice trasposta di B
Ridefinisci la matrice A eliminando la seconda colonna. Ridefinisci la matrice B eliminando la prima riga. Verifica che le matrici così ottenute abbiano la stessa dimensione.
Commenta i differenti risultati che otteniamo nelle operazioni A*B, B*A, A%*%B e B%*%A.
Assegna i seguenti nomi alle colonne e alle righe della matrice C: "col_1", "col_2", "col_3", "col_4", "row_1", "row_2", "row_3".

9.4 Array

Abbiamo visto come le matrici siano un oggetto bidimensionale, tuttavia è possibile anche creare oggetti che abbiano 3, 4 o un qualsiasi numero (n) di dimensioni. Tali oggetti sono definiti array e possono essere creati con il comando array() indicando il vettore di valori utilizzati per popolare l’oggetto e la grandezza di ciascuna delle sue dimensioni.

array(data = , dim = )

Ad esempio per creare un cubo di lato 3 contenete i valori interi dall’1 al 27 possiamo eseguire il seguente comando.

my_cube <- array(1:27, dim = c(3,3,3))
my_cube
## , , 1
## 
##      [,1] [,2] [,3]
## [1,]    1    4    7
## [2,]    2    5    8
## [3,]    3    6    9
## 
## , , 2
## 
##      [,1] [,2] [,3]
## [1,]   10   13   16
## [2,]   11   14   17
## [3,]   12   15   18
## 
## , , 3
## 
##      [,1] [,2] [,3]
## [1,]   19   22   25
## [2,]   20   23   26
## [3,]   21   24   27

Tutte le principali funzioni ed operazioni di selezione che abbiamo visto per le matrici ed i vettori posono essere eseguite in modo analogo anche con gli array. Il funzinonamento generale della selezione di elementi tramite parentesi quadre risulterà ora certamente pù chiaro. Per ogni dimensione vengono indicarti gli indici di posizioni desiderati. L’ordine all’interno delle parentesi quadre determina la specifica deimensione a cui ci si riferisce e le virgole sono utilizzate per separare gli indici delle diverse dimensioni.

my_hypercube[<dim-1>, <dim-2>, <dim-3>, ..., <dim-n>]

Vediamo ora alcuni semplici eempi di selezione.

## [1] 1
## [1] 1 2 3
##      [,1] [,2] [,3]
## [1,]    1    4    7
## [2,]    2    5    8
## [3,]    3    6    9
## , , 1
## 
##      [,1] [,2]
## [1,]    1    4
## [2,]    2    5
## 
## , , 2
## 
##      [,1] [,2]
## [1,]   10   13
## [2,]   11   14

E’ facilmente intuibile come le matrici non siano altro che un caso speciale di array con 2 dimensioni. Infatti i più attenti avranno notato che il valore "array" compariva insieme a "matrix" nel valutare la tipologia di oggetto.

my_matrix <- matrix(1:12, nrow = 2, ncol = 2)
is.array(my_matrix)
## [1] TRUE
class(my_matrix)
## [1] "matrix" "array"

Tuttavia nota come un semplice vettore non sia un array. Ricordiamo infatti che un vettore non possiede una dimensione (dim) ma semplicemente una lunghezza (length).

my_vector <- 1:12
is.array(my_vector)
## [1] FALSE
dim(my_vector)
## NULL